Key Points
For readers unfamiliar with QuickSort, you can read the last two paragraphs below to review the basic steps of QuickSort, its time complexity, and space complexity.
This article focuses on discussing one of the most crucial aspects of QuickSort: the choice of pivot.
Pivot Selection: The choice of pivot significantly impacts the performance of QuickSort. Common optimization strategies include random pivot selection, the median-of-three method, and Tukey’s Ninther. These methods aim to reduce the probability of the worst-case scenario and enhance the algorithm’s performance across various data distributions. A good pivot selection can prevent complexity from reaching O(n^2).
Experimental Results
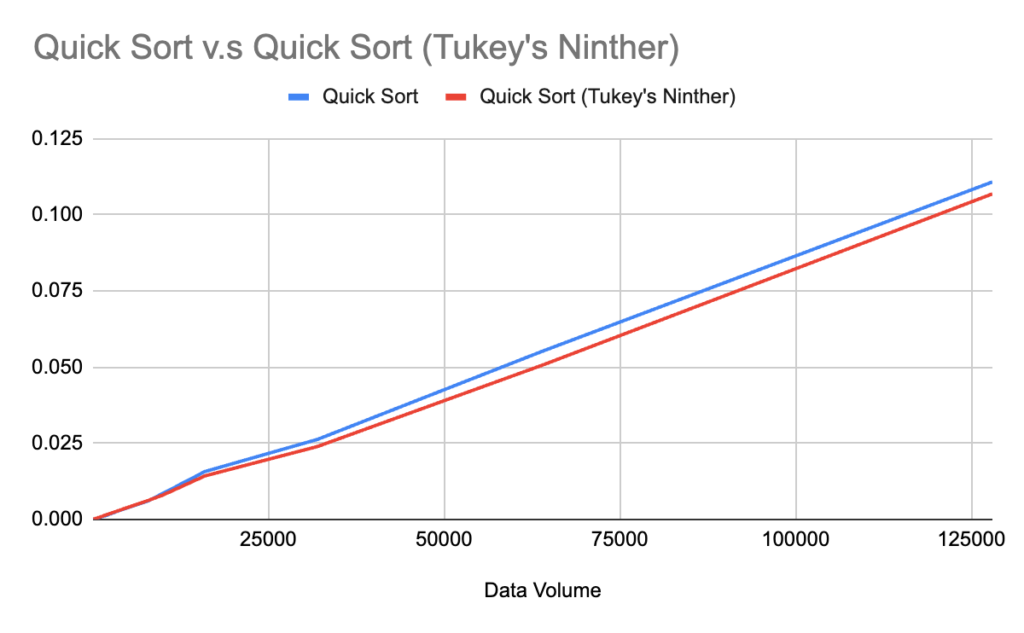
From the chart below, it can be seen that when the data volume exceeds 10,000 entries, in most cases, Tukey’s Ninther runs faster than QuickSort. The principle behind this is not difficult to understand; unlike traditional QuickSort, Tukey’s Ninther initially sets the median as the pivot through sampling, making the partitioning more balanced..
Readers interested in understanding the concept are recommended to watch this video on the median-of-three method, which is conceptually similar to Tukey’s Ninther but easier to understand.
Readers who have the time can also use my Performance Test to conduct actual tests.
Basic Steps
- Choosing the Pivot: Select an element from the array as the pivot, around which the sorting process will revolve.
- Partitioning: Rearrange the array so that all elements smaller than the pivot come before it, while all elements greater than the pivot come after it. After this partitioning, the pivot is in its final position.
- Recursive Sorting: Recursively apply quicksort to the parts of the array that are less than and greater than the pivot, respectively.
Time Complexity & Space Complexity
- Time Complexity:
- Best Case: O(n log n), when each partitioning divides the array into two roughly equal parts.
- Average Case: O(n log n), for randomly distributed data, the average performance of quicksort is very close to its best performance.
- Worst Case: O(n^2), when each partitioning operation divides the array into two parts, one of which contains all the elements while the other is empty, such as when the array is already sorted or all elements are the same.
- Space Complexity: The space complexity of quicksort is O(log n) because quicksort is performed recursively, requiring stack space to store the information of recursive calls. In the worst case, if the recursion tree becomes linear, the space complexity can reach O(n).
